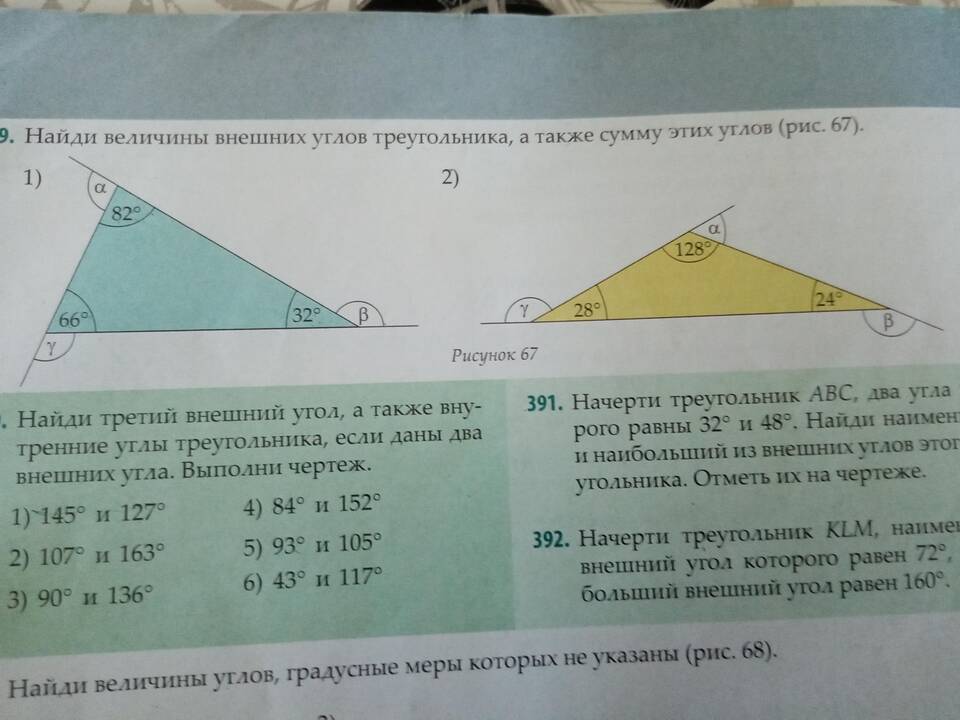
Внешним углом треугольника называется угол, смежный с внутренним углом треугольника. При каждой вершине треугольника можно построить два равных внешних угла.
Содержание
Определение внешнего угла треугольника
Теорема о сумме внешних углов треугольника
Сумма внешних углов треугольника, взятых по одному при каждой вершине, равна 360°.
Доказательство теоремы
Через сумму внутренних углов
- Сумма внутренних углов треугольника равна 180°: α + β + γ = 180°
- Внешние углы равны: α' = 180° - α, β' = 180° - β, γ' = 180° - γ
- Сумма внешних углов: (180° - α) + (180° - β) + (180° - γ)
- Упрощаем: 540° - (α + β + γ) = 540° - 180° = 360°
Графическое доказательство
- Если "пройти" вокруг треугольника, поворачиваясь на внешние углы
- Совершается полный оборот - 360°
- Следовательно, сумма внешних углов равна 360°
Пример расчета
| Внутренние углы | Внешние углы | Сумма внешних углов |
| 60°, 60°, 60° | 120°, 120°, 120° | 120° + 120° + 120° = 360° |
| 30°, 60°, 90° | 150°, 120°, 90° | 150° + 120° + 90° = 360° |
Свойства внешних углов
- Внешний угол равен сумме двух внутренних углов, не смежных с ним
- В равностороннем треугольнике все внешние углы равны 120°
- В прямоугольном треугольнике внешние углы при катетах равны 90° + противоположный угол
Важные замечания
| Условие | Примечание |
| Выпуклый многоугольник | Сумма внешних углов всегда 360° |
| Невыпуклый многоугольник | Теорема не применяется |
Практическое применение
- В навигации и картографии
- При расчетах в строительстве
- В компьютерной графике
- При решении геометрических задач